Numerical Reasoning Test: FREE Practice & Examples (2024)
All products and services featured are independently selected by WikiJob. When you register or purchase through links on this page, we may earn a commission.
- Numerical Reasoning Test – Free Practice
- What to Expect on a Numerical Ability Test in 2024
- Why Do Employers Use Numerical Reasoning Tests?
- What Makes Numerical Reasoning Tests Challenging?
empty
empty
empty
- Different Suppliers of Numerical Reasoning Tests
- Numerical Computation Questions
empty
empty
empty
empty
empty
empty
- Numerical Computation Practice Test
- Numerical Estimation Questions
- Numerical Estimation Practice Test
- Numerical Reasoning Questions
empty
empty
- Numerical Reasoning Practice Test
- Data Interpretation Questions
- Data Interpretation Practice Test
- Numerical Reasoning: Tips and Techniques for 2024
empty
empty
- Effective Strategies When Taking the Numerical Reasoning Test
- Frequently Asked Questions
- Final Thoughts
Numerical reasoning tests are used by employers to measure your ability to perform tasks involving numbers and are one of the core sections of any psychometric assessment test.
The questions range from simple arithmetic operations like addition and subtraction to more complex questions where you need to interpret numerical information presented as tables, diagrams and graphs.
Numerical ability tests are popular with employers because many jobs require you to work with numbers at least some of the time. If you are applying for a job which involves working with figures on a day-to-day basis, the employer will regard your numerical ability as a valuable predictor of your performance on the job.
In numerical reasoning tests, you will typically deal with graphs, tables, number sequences and text. These will contain the raw data needed to answer a written question, but you will often have to perform several operations on that data to arrive at the answer. They may also include questions where a mathematical problem is posed in words and your task is to apply the necessary logic to find the solution.
In graduate and management-level tests you will often be expected to answer data interpretation questions. These take the form of charts and graphs that you need to understand and then interpret. In other words, you need to work out how to get the answer rather than what calculations to apply.
Numerical Reasoning Test – Free Practice
To help you get an idea of what a numerical ability test involves, here is a practice test to get you started:
Credit: Psychometric Success
Prepare for Any Job Assessment Test with JobTestPrep
What to Expect on a Numerical Ability Test in 2024
There are two types of numerical questions that regularly appear in psychometric tests:
-
Speed questions – With unlimited time, most people taking theses tests could answer all the questions successfully. However, the time allowed to complete the test is so short that even the ablest person is not expected to finish. This means that the result depends on the number of correct answers made in the relatively short time allowed.
-
Power test – Contains questions that vary in difficulty; no one is expected to get all of the answers correct, even with unlimited time. In practice, a definite but ample time is set for power tests.
Some rarer forms of numerical reasoning tests have no time limit and/or negative scoring (incorrect answers subtract from your total score, rather than just scoring 0).
Depending on the provider, numerical reasoning tests could be taken at home or at an assessment centre; sometimes both – many organisations use an anti-cheating method that requires candidates to take another test at the assessment centre in person. If the home score and the in-person score are wildly different, then alarm bells start to ring.
The duration of any numerical ability test you are asked to take will depend on several factors including how many other tests you are taking on the day. However, most tests last about 30 to 40 minutes and have about 30 to 40 questions.
The questions used in numerical ability tests can be classified into four basic types:
-
Numerical computation – These questions involve the basic principles of arithmetic including addition, subtraction, multiplication, division, percentages, ratios, fractions and decimals. To score well on these questions, you need to make quick and accurate calculations without using a calculator.
-
Numerical estimation – Numerical estimation is essential in many technical jobs where you need to quickly and accurately make estimates of material quantities, etc. These questions require you to make quick estimates of the answers to straightforward numerical questions. You should not attempt to calculate the answers; this will take up too much time and prevent you from answering enough questions to get a good score.
-
Numerical reasoning – These questions test your reasoning ability rather than your ability to do calculations. In other words, you need to work out how to get the answer rather than simply being told what calculations to apply. They always include some number series questions where you need to work out which number or numbers are missing from the series. They also include text-based questions where a mathematical problem is posed in words and your task is to apply the necessary logic to find the answer.
-
Data interpretation – Most management and supervisory jobs require you to interpret data presented in charts, tables and graphs in order to make day-to-day decisions. These tests commonly use pie charts, line graphs, scatter-plots and tables of data which you need to interpret to answer the questions. The more complex questions may show the data in one format (such as a table) and a subset of this data in another format (such as a pie chart). To answer the questions, you need to be able to cross-reference these two elements logically.
This article has been designed so that it is easier for you to practise the areas where you feel that you are weakest, giving you the greatest benefit in the shortest time. So, each test contains more questions of each type than you would get in a real test.
It also ensures that you receive maximum exposure to as wide a variety of questions styles and types as possible. It’s important to remember that a real test will contain a mixture of question types.
Prepare for Any Job Assessment Test with JobTestPrep
Why Do Employers Use Numerical Reasoning Tests?
Psychometric tests have a long history of research behind them. A strong correlation between performance on these tests and performance in the workplace has led to companies all over the world investing in them as a crucial part of their recruitment process.
Many employers need to know that you have a solid foundation of basic mathematical skills.
These skills (calculating percentages, ratios, fractions, profit, revenue and so on) are crucial in almost any area of business.
Employers use numerical ability tests primarily because of:
- Their proven track record at indicating workplace performance
- Their use of mathematical skills that are relevant to the job you’re applying for
- The fact that these tests are quite fair in general
- They’re based on nothing but your raw ability and practice
For these reasons and more, many employers even say that they value these aptitude tests more than university degrees.
Company recruiters know that their new hires won’t necessarily have a great deal of industry or job-specific knowledge. That’s what comes with experience. The key for them is to choose applicants who have the foundations that allow them to adapt to the environment and pick up the skills and knowledge they need.
Companies are primarily interested in your grasp of the basics. They are also looking at how quickly you can work under pressure. This sort of arithmetic should be the kind you can do quickly and accurately whenever it is needed.
What Makes Numerical Reasoning Tests Challenging?
Numerical ability tests are often the most difficult aptitude test type for many candidates. This is for a few key reasons which we’ll outline here:
Time Limit
On average, you generally have between 45 seconds and 2 minutes to answer each question.
At the lower end of that scale, that’s really tough. There are many tests in which making it to the end is a feat in itself.
Having the ability and confidence to be able to interpret the data, decide what needs to be done and then perform those operations quickly is challenging, so practice is essential. We recommend the numerical practice packages from JobTestPrep.
Prepare for Any Job Assessment Test with JobTestPrep
Multiple Operations
Many questions won’t have a straightforward answer. You won’t, for example, only have to multiply two numbers to reach the solution.
This is an often-overlooked skill that only comes from practice. You might be a whizz at the actual addition, multiplication, percentages and so on, but you’ll still be left behind if you can’t quickly and accurately identify exactly which operations you need to do and in what order.
Maths
Sometimes the mathematical skills themselves can be difficult – especially if maths isn’t your strongest area.
When you factor in the previous two difficulties – the time limit and understanding how to answer the question – the pressure of the situation can very easily make it difficult to perform well.
Different Suppliers of Numerical Reasoning Tests
Not all numerical tests are created equal. While they all aim to test a similar set of skills, each test creator will have its own ideas about how best to go about that.
As part of your preparation, if you can find out what test provider the company you’re applying to is using, you’ll be able to focus your practice even more.
The main providers are:
- Capp Assessments
- Cubiks
- cut-e
- IBM Kenexa
- Pearson
- Saville
- SHL
- Talent Q
- Team Focus PFS
- Test Partnership
Two of the main test providers are SHL and Pearson, some of the oldest names in the industry. Their tests tend to set the industry standard, with many test suppliers following suit and only making relatively minor changes to the format. If in doubt, you can’t go wrong practising their tests.
With that said, some providers do shake things up.
For instance, Talent Q has an innovative test that adapts as you go. Your correct and incorrect answers help to inform the test of your skill level and it adjusts the questions accordingly. This allows the test to be flexible and short.
cut-e also stands out from the pack. With very short tests, between 5 and 12 minutes long, its questions focus on more abstract, mathematical elements rather than graphs and charts. This can confuse candidates who are used to working with more practical types of questions.
Which supplier a company uses sometimes depends on the specific role and department. Of course, you should always bear in mind that companies can choose to change supplier at any time.
Always ensure you build up the essential skills you need that apply to any numerical reasoning test. It’s those skills that are being examined, not specific knowledge of a particular test. Being able to think on your feet and adapt to changes is also something most employers will be looking for.
Numerical Computation Questions
Numerical computation questions involve mathematical terms and methods, and basic principles of arithmetic, such as:
- Addition
- Subtraction
- Multiplication
- Division
- Percentages
- Ratios
- Fractions
- Decimals
This type of test can be categorised as a speed test and is used to determine your basic numeracy. You will not be allowed to use a calculator.
If you are very rusty with arithmetic, try re-learning the times tables up to 12 and practise multiplication, division and percentage calculations. Practice can improve your test scores for all types of aptitude tests, so try as many examples as you can.
These questions are directly applicable to many administrative and clerical jobs, but can also appear as a component of graduate and managerial tests.
The speed at which you can answer these questions is the critical measure, as most people could achieve a very high score given unlimited time in which to answer. You can, therefore, expect 25 to 35 questions in 20 to 30 minutes.
Simple Arithmetic
You can achieve a big improvement in your scores by practising your mental arithmetic until you are both quick and confident. Your score in the simple speed tests will be very much influenced by your ability to add, subtract, multiply and divide quickly and accurately.
In a typical test of 60 mixed questions, you may need to perform over 200 separate multiplication and division operations. Knowing your multiplication tables (up to the ten times table) and being able to give an instant answer to any operation is essential.
The key word here is ‘instant’. Most people can provide instant answers to about 80% of these operations and take a few seconds to think about the remainder. These extra few seconds add up over the course of the test, where answering a single question can involve three or four of these simple operations.
Shaving a few seconds off here and there gives you time to answer an extra four or five questions in a typical test – and this will make a big difference to your final score.
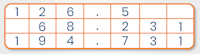
You are very unlikely to have any problems with the 1, 2, 5 and 10 times tables – so you can probably ignore them.
Take a sheet of A4 paper and list the numbers 3, 4, 6, 7, 8, 9 in a column down the left-hand side of the page and along the top margin as shown:
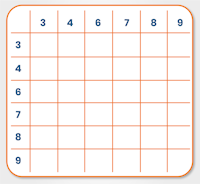
Work from left to right and top to bottom through the grid, writing in each answer. If you pause for even a second to think about the answer then place a dash in the space and continue.
Do not stop to think. Either write the answer immediately or put a dash in the space. You must complete this exercise in less than 40 seconds.
The result is usually a sheet with a few dashes, where the correct answer did not come instantly to mind. You will need to spend a bit of time refreshing your memory on these operations – do this over a few days, spending a couple of minutes at a time until they are instantaneous.
When you are completely happy, try the grid again – you should be able to complete it correctly in fewer than 40 seconds.
The rules for performing basic arithmetic operations with whole numbers (integers) should be familiar to you, although you may find that there are some things you have forgotten. For example:
- Multiplication or division of two integers with different signs gives a negative result; for example:
- Multiplication or division of two negative integers gives a positive result; for example:
There are some tips and tricks to help you with your mental arithmetic that are worth spending time practising.
They will all make a small difference to your overall speed; if you can master a few of them, and they are all straightforward, then the cumulative effect will enable you to answer a few more questions in the allotted time.
As you already know, these few extra marks can make a big difference in how you are perceived as a job candidate.
Subtraction
Consider the sum: . There are three approaches to this type of calculation:
1. Direct Calculation
When the digits of ‘b’ are all smaller than the digits of ‘a’, the calculation can be done digit by digit.
For example:
Evaluate 862 – 41 simply by subtracting 1 from 2 in the units place and 4 from 6 in the tens place. This equals 821.
2. Indirect Calculation
When the above situation does not apply, the problem can sometimes be modified:
If only one digit in ‘b’ is larger than its corresponding digit in ‘a’, diminish the offending digit in ‘b’ until it is equal to its corresponding digit in ‘a’.
Then subtract further the amount ‘b’ was diminished by from ‘a’.
For example:
To calculate , turn the problem into .
Then subtract 20 from 800 = 780.
If more than one digit in ‘b’ is larger than its corresponding digit in ‘a’, it may be easier to find how much must be added to ‘b’ to get ‘a’.
For example:
To calculate 8,192 – 732, we can add 8 to 732 (resulting in 740), then add 60 (to get 800), then 200 (for 1,000).
Next, add 192 to arrive at 1,192 and, finally, add 7,000 to get 8,192. Our final answer is 7,460.
3. Look-Ahead Borrow Method
This method can be used to subtract numbers left to right and, with a little practice, it can dramatically speed up mental subtraction.
One place at a time is handled left to right.
Example:
4,075
– 1,844
Thousands:
, look to the right, 075 < 844, need to borrow.
, say, “Two thousand”
Hundreds:
0 – 8 = negative numbers not allowed here
75 > 44 so no need to borrow, say, “Two hundred”
Tens:
5 > 4 so no need to borrow, say, “Thirty”
Ones:
, say, “One”
This gives 2,231 as the answer.
Multiplication
Calculating products:
1. Multiplying by 2
In this case, the product can be essentially calculated digit by digit.
This is not exactly the case because it is possible to have a remainder. If there is a remainder, it is always 1, which simplifies things greatly. Still, the product must be calculated from right to left:
2 x 167 is by 4 with a remainder, then a 2 (so 3) with another remainder, then a 2 (so 3).
Thus, we get 334.
2. Multiplying by 5
To multiply a number by 5, multiply that number by 10 and then divide it by 2. The following algorithm is a quick way to produce this result:
- First, append a zero to the right side of the desired number
- Next, starting from the leftmost numeral, divide by 2 and append each result in the respective order to form a new number
- Fraction answers should be rounded down to the nearest whole number
For example, if you intended to multiply 176 by 5, you would first append a zero to 176 to make 1,760.
Next, divide 1 by 2 to get 0.5 rounded down to 0
Divide 7 by 2 to get 3.5, rounded down to 3
Divide 6 by 2 to get 3
0 divided by 2 is simply 0
The resulting number is 0330
The final step involves adding 5 to the number that follows any single numeral in this new number that was odd before dividing by two; this is better understood through the example:
In the original number, 176, the first place is 1, which is odd. Therefore, we add 5 to the numeral after the first place in our newly constructed number (0330), which is 3:
The numeral in the second place of 176, 7, is also odd. Therefore, the number-place after the corresponding numeral in the constructed number (0830) is increased by 5 as well.
The numeral in the third place of 176, 6, is even, therefore the final number, 0, in our answer is not changed. That final answer is 0880. The leftmost zero can be omitted, leaving 880.
So,
3. Multiplying by 9
Since , to multiply by 9, multiply the number by 10 and then subtract the original number from this result.
For example,
4. Multiplying Two 2 Digit Numbers Between 11 and 19
To easily multiply two-digit numbers together between 11 and 19, you can use this simple grid method:
Consider the calculation
This can be visualized as:
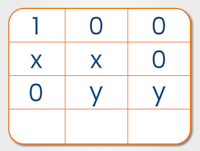
So, for example, the calculation 17 x 16 can be visualized as:
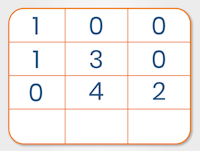
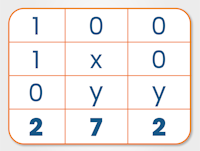
Adding the columns in the grid gives the answer 272, like this:
5. Multiplying Any Two-Digit Numbers Together
To easily multiply any two-digit numbers together, a simple algorithm is as follows:
For example, can be reduced to:
800 (which is 2 x 4 x 100)
120 (which is 3 x 4 x 10)
140 (which is 7 x 2 x 10)
21 (which is 7 x 3)
Adding these gives 1,081.
You will need to practise these methods a few times to become proficient, but they can save significant time answering numeric calculation and estimation questions.
Fractions
A fraction is a number of the form a/b, where ‘a’ and ‘b’ are integers.
The ‘a’ is called the numerator of the fraction and ‘b’ is called the denominator.
For example, 3/5 is a fraction that has ‘3’ as its numerator and ‘5’ as its denominator. This can be thought of as 3 divided by 5.
If the numerator and denominator of the fraction are both multiplied by the same integer, the resulting fraction will be equivalent. If the numerator and the denominator of the above fraction are multiplied by 5 then this gives 15/25.
Therefore,
1. Adding, Subtracting and Comparing Fractions
To add two fractions with the same denominator, you simply add the numerators and keep the denominator the same.
If the denominators are not the same, you need to make them the same before doing the addition. To do this, you need to get the lowest common denominator.
In mathematics, the lowest common denominator (abbreviated LCD) is the lowest common multiple of the denominators of a set of fractions. That is, it is the smallest (non-zero) number that is a multiple of the denominators.
For instance, the LCD of 1/2 and 1/4 is 4 because the lowest common multiple of 2 and 4 is 4.
Remember, the denominator says what the numerator is ‘divided by’. Any number divided by 4 will be lower than if it were divided by 2. Therefore, 4 is the lowest common denominator.
Likewise, the LCD of 1/2 and 1/3 is 6 because the smallest (non-zero) number that is a multiple of 2 and 3 is 6.
Using the LCD (or any multiple of it) as a denominator enables addition, subtraction or comparison of fractions.
For example:
since
2. Subtracting Fractions
The process for subtracting fractions is, in essence, the same as that of adding them – find a common denominator and change each fraction to an equivalent fraction with the chosen common denominator.
The resulting fraction will have that denominator and its numerator will be the result of subtracting the numerators of the original fractions.
For instance:
3. Multiplying Fractions
To multiply two fractions, multiply the two numerators and multiply the two denominators (the denominators need not be the same).
For example:
4. Multiplying Fractions by Whole Numbers
If you have a quarter of a cake and you multiply the amount by three, then you end up with three quarters. We can write this numerically as follows:
As another example, suppose that five people work for three hours out of a seven-hour day (i.e. for three-sevenths of the workday).
In total, they will have worked for 15 hours (5 x 3 hours each) or 15-sevenths of a day.
Since seven-sevenths of a day is a whole day, 14-sevenths is two days. Then, in total, they will have worked for two days and one-seventh of a day.
Numerically:
5. Multiplying Fractions by Fractions
Consider the cake example again; if you have a quarter of a cake and you multiply the amount by a third, you end up with a twelfth of the cake.
In other words, a third of a quarter (or a third times a quarter) is a twelfth. This is because each quarter is split into three pieces, and four quarters times three makes 12 parts (or twelfths).
We can write this numerically as follows:
When fractions are multiplied by fractions, simply multiply the two numerators (the top numbers) and multiply the two denominators (the bottom numbers).
For example:

If you need to prepare for a number of different employment tests and want to outsmart the competition, choose a Premium Membership from JobTestPrep.
You will get access to three PrepPacks of your choice, from a database that covers all the major test providers and employers and tailored profession packs.
Prepare for Any Job Assessment Test with JobTestPrep
6. Dividing Fractions
To divide one fraction by another, invert the fraction you are dividing by and then proceed as in multiplication.
For example:
7. Mixed Numbers and Improper Fractions
In the example above, an expression such as 1½ is called a mixed number. It means 1 plus 1/2.
For instance, you could have two entire cakes and three-quarters of another cake. The whole and fractional parts of the number are written next to each other:
Whenever you are asked to perform calculations with mixed numbers you may find it easier to convert the mixed number to an improper fraction.
An improper fraction can be thought of as another way to write a mixed number; in the ‘2¾’ example above, imagine that the two entire cakes are each divided into quarters.
Each entire cake contributes 4/4 to the total, so is another way of writing 2¾.
A mixed number can be converted to an improper fraction in three steps:
- Multiply the whole part times the denominator of the fractional part
- Add the numerator of the fractional part to that product
- The resulting sum is the numerator of the new (improper) fraction, and the new denominator is the same as that of the mixed number
Similarly, an improper fraction can be converted to a mixed number:
- Divide the numerator by the denominator
- The quotient (without remainder) becomes the whole part and the remainder becomes the numerator of the fractional part
- The new denominator is the same as that of the original improper fraction
For example, if you are asked to solve the following:
Convert 7 to an improper fraction: 57/8
Convert 2 ¾ to an improper fraction: 11/4
Determine the LCD: which is 8
Convert: 11/4 to 22/8
Calculate:
Convert: 35/8 to 4⅜
Therefore,
Decimals
All numbers can be expressed in decimal form using base 10. A decimal point is used and the place value for each digit corresponds to a power of 10, depending on its position relative to the decimal point.
For example, the number 62.437 has 5 digits, where:
‘6’ is the ‘tens’ digit; the place value for ‘6’ is 10
‘2’ is the ‘units’ digit; the place value for ‘2’ is 1
‘4’ is the ‘tenths’ digit; the place value for ‘4’ is 1/10
‘3’ is the ‘hundredths’ digit; the place value for ‘3’ is 1/100
‘7’ is the ‘thousandths’ digit; the place value for ‘7’ is 1/1,000
Therefore, 82.537 is a short way of writing:
This numeration system has implications for basic operations. For addition and subtraction, you must always remember to line up the decimal points:
For example:
can be written with the decimal points aligned as:
To multiply decimals, it is not necessary to align the decimal points.
To determine the correct position for the decimal point, you simply add the number of digits to the right of the decimal points in the decimals being multiplied.
For example:
In this example, the first number has three decimal places, the second number has two decimal places and, therefore, the answer must have five decimal places.
To divide a decimal by another, such as 62.744 ÷ 1.24, first move the decimal point in the divisor to the right until the divisor becomes an integer, then move the decimal point in the dividend the same number of places.
This gives
This procedure determines the correct position of the decimal point in the quotient (as shown). The division can then proceed as normal.
Conversion of Decimals and Fractions
Conversion from a given decimal to an equivalent fraction is straightforward. Since each place value is a power of ten, every decimal can be converted easily to an integer divided by a power of ten.
For example:
The last example can be reduced to lowest terms by dividing the numerator and denominator by 4, which is their greatest common factor.
The greatest common factor of two non-zero integers is the largest positive integer that divides both numbers without a remainder.
So,
Therefore,
Any fraction can be converted to an equivalent decimal. Since the fraction a/b means ‘a’ divided by ‘b’, we can divide the numerator of a fraction by its denominator to convert the fraction to a decimal.
Percentages
A percentage is a way of expressing numbers as fractions of 100 and is often denoted using the per cent sign (%).
For example, 45.1% (read as ‘forty-five point one per cent’) is equal to 0.451.
Percentages are used to express how large one quantity is in terms of another quantity. The first quantity is then usually a part of or a change in the second quantity.
For example, an increase of $0.15 on a price of $2.50 is an increase by a fraction of .
Expressed as a percentage, this is, therefore, an increase of 6%.
1. Percentages May Be Relative
Due to inconsistent usage, it is not always clear from the context what a percentage is relative to. When speaking of a ‘10% rise’ or a ‘10% fall’ in a quantity, the usual interpretation is that this is relative to the initial value of that quantity.
For example, a 10% increase on an item initially priced at $200 is $20, giving a new price of $220. To many people, any other usage is incorrect.
In the case of interest rates, however, it is a common practice to use the per cent change differently:
Suppose that an initial interest rate is given as a percentage like 10%. Suppose the interest rate rises to 15%. This could be described as a 50% increase, measuring the increase relative to the initial value of the interest rate.
However, many people say in practice, "The interest rate has risen by 5%".
To counter this confusion, the unit ‘percentage points’ is sometimes used when referring to differences of percentages. So, in the previous example, "The interest rate has increased by 5 percentage points" would be an unambiguous expression that the rate is now 15%.
With changes, percentage can be of any positive value. For example, a 100% growth is synonymous with doubling; a growth of 100% starting from 200 units is 200 units, increasing the total to 400.
2. Percentages and Cancellations
A common error when using percentages is to imagine that a percentage increase is cancelled out when followed by the same percentage decrease.
A 50% increase from 100 is 100 + 50, or 150
A 50% reduction from 150 is 150 – 75, or 75
The result is smaller than the 100 we started with.
This phenomenon is due to the change in the initial value after the first calculation. In this example, the first initial value is 100 but the second is 150.
In general, the net effect is:
that is a net decrease proportional to the square of the percentage change.
To use a specific example, stockbrokers came to understand that even if a stock has sunk 99%, it can nevertheless still sink another 99%.
Also, if a stock rises by a large percentage, the trader still loses all of the stock's value if the stock subsequently drops 100%, meaning it has a zero value.
Numerical Computation Practice Test
Credit: Psychometric Success
Prepare for Any Job Assessment Test with JobTestPrep
Numerical Estimation Questions
Numerical estimation questions test your ability to make quick estimates of the answers to fairly straightforward numerical questions. To score well on these questions, you will need to make quick approximations of the answer.
You must avoid the trap of working out the answer exactly, which will take up too much time and prevent you from answering enough questions to get a good score.
Numerical estimation is vital in many craft and technical jobs, where the ability to quickly and accurately estimate material quantities is essential.
However, the ability to make quick estimates is a useful skill to have even if you are sitting a graduate or professional level test, as it will enable you to roughly check your answers to data interpretation questions.
The speed at which you can answer these questions is the critical measure, as most people could achieve a very high score given unlimited time in which to answer. You can, therefore, expect 25 to 35 questions in 10 minutes or so.
Even though numerical estimation questions appear straightforward, it can take some time to develop the optimum compromise between speed and accuracy.
Example question:
29 + 41 + 38 + 31 = ?
A) 130
B) 120
C) 160
D) 110
E) 140
Before you attempt to answer each question, look at the range of answers available and ask yourself how accurate your estimate needs to be. For example, is an order of magnitude sufficient or does the answer need to be worked out to the nearest whole number?
If you are out of practice with arithmetic, try relearning the times tables up to 12 and practise rough and ready multiplication, division and percentage calculations.
Practice can improve your test scores for all types of aptitude tests, but numerical estimation is one area where it can make a difference, so try as many examples as you can.
Numerical Estimation Practice Test
Credit: Psychometric Success
Prepare for Any Job Assessment Test with JobTestPrep
Numerical Reasoning Questions
Numerical reasoning tests require you to interpret some given information and then apply appropriate logic to answer the questions. In other words, you need to work out how to get the answer rather than what calculations to apply.
Sometimes, the questions are designed to approximate the type of reasoning required in the workplace.
The most popular type of numerical reasoning questions are number series questions.
Numerical reasoning questions are very commonly used in graduate and managerial selection. You can usually expect 15 to 20 questions in 20 to 30 minutes.
Numerical reasoning is an increasingly popular way of assessing candidates during the job selection process. Many people who have been out of the education system for a while or who don’t use maths on a day-to-day basis feel intimidated by these types of test.
The important thing to remember is that you don’t need to have studied mathematics to a high level to do well in these tests. They are primarily tests of reasoning ability and the math needed is invariably straightforward. Having said that, you may need to get up to speed with percentages, ratios, proportions, fractions and decimals.
You will usually be allowed to use a calculator for these types of question and investing in one which can handle fractions and percentages is a good idea. You should also try to work through a few numerical computation practice papers to get back into the swing of these types of calculation.
Understanding Number Sequences
These questions require you to find the missing number in a sequence of numbers. This missing number may be at the beginning or middle but is usually at the end.
For example:
1. Find the next number in the series
4, 8, 16, 32...
A) 48
B) 64
C) 40
D) 46
2. Find the missing number in the series
54, 49, …, 39, 34
A) 47
B) 44
C) 45
D) 46
These number sequences can be quite simple like the examples above. However, you will often see more complex questions where the intervals between the numbers are the key to the sequence.
3. Find the next number in the series
3, 6, 11, 18…
A) 30
B) 22
C) 27
D) 29
4. Find the next number in the series
48, 46, 42, 38…
A) 32
B) 30
C) 33
D) 34
These simple number sequences usually consist of four visible numbers plus one missing number. This is because the test designer needs to produce a sequence into which only one number will fit.
The need to avoid any ambiguity means that if the number sequence relies on a more complex pattern then there will need to be more visible numbers.
For example:
5. Find the missing number in the series
4, 3, 5, 9, 12, 17, ?
A) 32
B) 30
C) 24
D) 26
6. Find the missing numbers in the series
5, 6, 7, 8, 10, 11, 14, ?, ?
A) 19
B) 17
C) 15
D) 16
To solve these number sequence questions efficiently, you should first check the relationship between the numbers themselves, looking for some simple arithmetic relationship.
Then look at the intervals between the numbers and see if there is a relationship there. If not, and particularly if there are more than four numbers visible, then there may be two number sequences interleaved.
You will occasionally find multiplication, division or powers used in these sequences, but test designers tend to avoid them as these operations soon lead to large numbers which are difficult to work out without a calculator.
Understanding Letters of the Alphabet as Numbers
Another type of sequence question which appears in these tests involves the substitution of letters of the alphabet for numbers.
For example:
A = 1, B = 2, etc.
It may seem strange to consider these as numerical reasoning questions but they work in the same way once you have changed them back into numbers.
1. Find the next letter in the series
B, E, H, K, ?
i) L
ii) M
iii) N
iv) O
2. Find the next letter in the series
A, Z, B, Y, ?
i) C
ii) X
iii) D
iv) Y
Because arithmetic operations cannot be performed on letters, there is less room for ambiguity in these questions. This means that interleaved sequences can be used with fewer visible letters than in questions that use numbers.
It is implicit in these ‘alphabetic sequence’ questions that the sequence ‘loops’ back around and starts again. It is important to recognize this as it is not usually stated explicitly – you are just expected to know it.
If you see more than one of these questions in a test, it is almost certainly worth taking the time to write out the letters of the alphabet with their ordinal numbers underneath.

You can then treat these questions in a similar way to number sequence questions. This can save a lot of time overall and avoids simple mistakes.
Numerical Reasoning Practice Test
Credit: Psychometric Success
Prepare for Any Job Assessment Test with JobTestPrep
Data Interpretation Questions
The ability to interpret data presented in tables, graphs and charts is a common requirement in many management and professional jobs.
If you are applying for a job which involves analysis or decision-making based on numerical data, then you can expect to have to answer data interpretation questions.
Data interpretation problems usually require two basic steps:
- First, you have to read a chart or graph to obtain certain information
- Then you have to apply or manipulate the information to obtain an answer
These questions often use very specific illustrations; for example, the question may present financial data. However, an understanding of finance will not be needed to answer the question.
You can usually expect 20 to 25 questions in 20 to 30 minutes.
Candidates who have been out of the education system for a while or who don’t need to interpret graphs, pie charts, scatter diagrams and tables of data on a day-to-day basis may feel overawed by these types of questions.
The important thing to remember is that you don’t need to have studied mathematics to a high level to succeed. These questions are primarily tests of interpretation and the math needed is invariably straightforward.
You are usually allowed to use a calculator in data interpretation tests.
Data Interpretation Practice Test
Prepare for Any Job Assessment Test with JobTestPrep
Numerical Reasoning: Tips and Techniques for 2024
Most tests allocate one mark to each correct answer – there is no differential marking.
This means that you will get one mark for calculating a percentage or fraction and you will get one mark for understanding some data presented graphically and answering a question about it.
Therefore, it makes sense to concentrate on improving your mental arithmetic and making sure that you are familiar with percentages, fractions, ratios, etc. as these can gain you easy marks.
Also, do not linger on questions that you find difficult – if you can, complete all those you can answer easily and then go back and fill in the gaps.
Practising for Your Test
The very first step is to research your test. Read everything you can about numerical tests in general and see if you can find out exactly what kind of tests the company you’re applying to uses.
Also, check out forums or ask friends who’ve taken the test for any tips. This will help you to focus your practice and make it much more efficient, as well as getting used to the format you’ll be faced with.
Once you think you have a good grasp of what you’re up against, the next step is to simply practise, practise and practise. Run through sample questions and full mock tests, such as the numerical test packages from JobTestPrep.
Prepare for Any Job Assessment Test with JobTestPrep
For at least some of your practice, you should answer questions under test conditions. In particular, you need to get used to timing yourself and sticking to strict time limits.
If you have 30 minutes to answer 30 questions, you need to make sure you don’t spend longer than a minute per question on average.
You can do this by using a stopwatch. Every time it reaches a minute (or whatever the average time is), reset it and move on. Come back to the ones you didn’t finish if you have time at the end. This will help you to not be flustered by the pressure of the test itself.
Once you’re used to the format and the questions, the actual test is just a matter of staying calm and getting it done.
It’s always good to search widely for resources that can help you prepare for your numerical reasoning assessment.
Here are some of our suggestions for additional resources that are worth looking into:
-
Apps – We’ve created a psychometric tests app, available for both Apple and Android. It contains questions that simulate the ones published by SHL, Kenexa, CAPP and Cubiks, among others. It has a built-in timer, and afterwards, you can check out the solutions with workings to learn and progress.
-
Online Practice Tests – As well as our own aptitude tests, WikiJob recommends the numerical test packages available from JobTestPrep. JobTestPrep offers a wide range of professionally designed numerical reasoning practice packs, questions, tests and resources. The questions are structured in a professional format, just like the real thing. Practice numerical tests are also offered by other providers like Psychometric Success.
Just Before the Test
First, make sure that you’ve had plenty of sleep, plenty of water and something to eat. Remember to bring the following with you:
- A calculator (if allowed)
- A stopwatch
- Some scrap paper and a pencil
- Some water
If you’re doing the test at home then find a quiet, private room you can sit in. Make sure you won’t be disturbed and check that your internet is stable.
Take a deep breath, stay calm and start your test.
Effective Strategies When Taking the Numerical Reasoning Test
If you’ve practised and prepared well then hopefully taking the real test should feel familiar. Just with a little more pressure.
Do things exactly as you’ve prepared. Calculate the average time you have per question and use your stopwatch to stay on time.
Here are a few things to remember as you take your test:
Step 1. Use the Practice Questions to Your Full Advantage
Often, you’ll be given a couple of example questions at the start of your test to make you aware of the format and so you can orientate yourself. How are the questions posed? What is the data like? What kind of calculations need to be done? Jot down anything you think might help you going forward. This will also be the last chance you have to ask any questions you might have before the test begins.
Step 2. Read the Questions Carefully
Don’t let the time limit stop you from reading thoroughly. This is particularly important because misunderstandings are often the cause of forgetting to do a particular step in a calculation or not answering the question. Read every question twice and make sure you read the information provided carefully as well.
Step 3. Don’t Make Assumptions
Remember that everything you need to answer the question is on the page and nowhere else. If you happen to remember a figure or a fact from your research elsewhere that seems like it could be relevant, ignore it. Also, use this knowledge to encourage you. If an answer seems impossible to find, you know for sure that it is possible based only on what’s on the page.
Step 4. Use a Process of Elimination
If you’re really stuck, look at some of the multiple-choice answers you’re given and work backwards. See if there are any answers that definitely look like they can’t be the answer and eliminate those first.
Step 5. Focus
A key skill that the numerical assessment aims to test is your ability to scan data and hone in on what’s important. That’s why you must read the question carefully so that you know what you need to find out. Then read the context carefully. What data does the table contain? What does the graph show? Figure out what data you can ignore and concern yourself only with the information that will help you to answer the question.
Step 6. Make Notes
Have your scrap paper beside you and make use of it. It can quickly become overwhelming having to juggle a lot of data and information in your head. Save yourself the trouble and write down the facts you think are important as you work through the question.
Step 7. Always Check Units, Currencies and Bases
A very common slip-up in numerical tests is to get units of measurements, currencies, etc. confused. Sometimes, you will need to convert between currencies. Using two figures as if they were the same currency will send you straight to the wrong answer. The same goes for graphs, tables and charts. Always check the axes, what they represent and if there are any abbreviations (such as writing ‘10’ on the graph, when the axis explains it refers to ’10 million’). It seems obvious, but in the heat of the moment, these things can be easily forgotten.
Step 8. Ignore Other Test-Takers
If you’re taking a test in person at an assessment centre, it’s likely that you won’t be alone in the room. Don’t let it get to you. Other candidates might be sighing or fidgeting or rustling paper or looking around. It doesn’t matter – you’re there for your test and your test only. There’s no time to be distracted, so keep your head down and focus on your own numerical test.
A numerical reasoning test is an assessment that is commonly used in the application process for different jobs.
It is used to assess the numerical aptitude of a candidate to screen applicants by their inherent knowledge, skills and abilities to ensure that they have what it takes to be successful in the advertised role.
The numerical reasoning test is usually a multiple-choice test where numerical data is presented in the form of tables and graphs, with a question that requires some simple mathematical operation to be completed to find the correct answer. They are usually completed remotely with a short time limit.
Although the questions are regarding numerical data, this is not a maths test – instead, it is an assessment of how competent and confident you are when dealing with and manipulating data. It is about how you approach a problem logically and can use basic mathematical concepts.
If you are facing a numerical reasoning test, getting prepared will give you the best chance to get through to the next stage of the recruitment process.
Practicing numerical reasoning tests can help in several ways. Not only will they make you more familiar with the structure and layout of the assessments, but they will also give you an idea of what to expect in terms of the content, too.
If you know the publisher of the test you will be facing, you can find practice tests that contain the same type of questions in the same format, with the right time limit. This is the most effective way to practice.
When you have completed some practice tests, you will be able to see if there are any mathematical concepts or operations that you need to refresh your memory on. In most cases, the operations are built on the knowledge you will have gained from secondary-level education – multiplication, addition, division and subtraction, as well as fractions, percentages and ratios. Focus your revision on the areas where you struggle the most to get the best results.
On the day of the assessment, make sure that you have had a good night’s sleep and that you are well fed and hydrated. This will help your brain to work at full capacity and give you a greater chance.
In general, it’s best to go for accuracy. Even if you are taking a speed test, accuracy is just as important. For most tests, the employer will receive an accuracy score as well as your raw score.
They will be more interested in a candidate who took slightly longer but was much more accurate, than a candidate who raced through but was sloppy.
What feedback you get and when varies a lot from company to company. Some provide you with no feedback, some only if you succeed, some offer a summary to all candidates.
Depending on the kind of feedback offered, this can happen instantly after you complete the test (an automated feedback system) or anywhere from a few days to a few weeks after completing the test.
If you’re unsure whether or not you will get feedback or when you should receive it, just ask the company’s HR team.
When taking a speed test like numerical estimation or numerical computation, you will not be allowed to use a calculator. These tests require you to work through easy maths questions at a fast pace and test your mental arithmetic.
You will usually be allowed to use a calculator for numerical reasoning and data interpretation questions.
The majority of tests conducted in person at an assessment centre will have calculators provided, but always bring your own just in case. It’s always best to use a calculator you’re familiar with.
The type of calculator that you use can help or hinder you enough to make a difference to your scores. Specifically, the calculator you use should:
- Have a large keypad as this will minimise keying errors
- Have percentage and memory functions
- Not be over complex with several functions assigned to each key
- Display the last few figures and any associated operators (+, –, x, ÷, etc.) This means that you can check your input at a glance if you think that you may have made a keying error
- Be familiar to you. That is you should have used it on a few practice papers before the real test
You probably won’t be allowed to if taking the test in person, but it wouldn’t help anyway.
The tests are designed so that all you need is your calculator and your own numerical ability. There’s no time to find answers on Google or forums.
Not a good idea.
Getting someone else to take the test for you might help you make it past the unsupervised online tests and through to the next stage of the process (assuming, of course, that the individual is actually better at the test than you) but employers aren’t stupid, and they won’t be fooled in the long run.
It’s very common that at the assessment centre stage you’ll be asked to take another set of aptitude tests, supervised and in person. The result of this test will be compared against your original online test and analysed. If you have cheated, you will most likely be found out at this stage.
And that’s just one of many anti-cheating methods employers have. Many of them aren’t publicised, because if they were then cheaters could look for ways around them.
Don’t take the risk. Putting in the practice is a much more effective and rewarding strategy.
As with many other aptitude tests, numerical reasoning tests are hard because they are used to screen applicants for a role.
However, the content of the test is not necessarily difficult – the mathematical operations that you need to use to find the right answer are GSCE-level, rather than degree-level.
What makes the numerical reasoning assessment difficult is the exam conditions that you have to contend with when you are taking them. When a test is one of the things that stands between you and your ideal role, it is usual to be nervous about completing the test.
In addition, numerical reasoning tests are usually designed with a tight time limit – adding extra pressure.
To give yourself the best chance, practice tests will help negate the difficulties posed by the real assessment. You will get used to the structure of the test and the time limit, the way you need to answer, and the type of questions that you will face. You can revise the problems that you find hardest so you can feel more confident.
There are many different types of numerical reasoning tests and almost as many different publishers of these tests. The time it takes to complete them differs slightly, too.
In most cases, the numerical reasoning test is quite brief, with a time limit of between five and 30 minutes.
Sometimes, the numerical reasoning test is part of a battery of aptitude assessments that are used to screen applicants for a role, which means that it might take a longer time to complete the tests.
There are different places online where you can practice numerical reasoning tests, and some offer free practice opportunities, while others offer paid preparation materials including revision, tips and tests.
This article provides a great start for your knowledge of what to expect, and the example questions are a good indication of the content that you might be faced with.
If you know which publisher is producing the assessment that you will be facing, then most will have a candidate hub – this is a great resource for revision, and often includes a highly accurate practice test that provides the exact information that you need.
If you do not know the publisher, or you want to widen your practice, then sites like JobTestPrep have a wide range of both free and paid resources that can help. The Prep Packs contain revision materials, tips and tricks for success, and a wealth of other information as well as practice tests.
In most cases, numerical reasoning tests need to be completed without a calculator – you will usually be allowed to use scrap paper to make notes if you need to.
As the content of the assessment is based on mental math skills, as a rule, calculators are not usually needed.
If the numerical reasoning test that the recruitment team is using does allow calculators and you plan on using one, it is a good idea to practice with it first.
Sometimes the calculations that you need to make to get to the correct answer are slightly different when you use a calculator, and the logic of an equation might be in an unfamiliar order, for example.
The types of question that you are likely to face in a numerical reasoning test depends largely on the publisher – and the job role that you are applying for.
Financial roles might have questions about accounting practices and financial reports, for example, while management roles might be looking at profit and loss or staffing issues.
Most of the questions in the numerical reasoning test are based on numerical data which is presented in graphs and tables. The answers are multiple-choice usually.
You might need to use multiplication, division, addition or subtraction to answer the questions. There are likely to be questions that need you to confidently use percentages, fractions and decimals to answer, and a working knowledge of ratios is a good idea.
The main difficulty in a numerical reasoning test is the exam conditions pressure – including a short time limit. You need to be able to confidently analyze and manipulate the numerical data quickly to answer correctly and give yourself the best chance for success.
Numerical reasoning tests are usually used as part of a recruitment process. To get through to the next stage, you will need to pass the test – but a good score depends on several factors.
Some tests are marked positively – which means that you earn marks for every correct answer. Some tests have negative marking, which means that you can lose marks for incorrect answers. Knowing whether the test you will be taking is negatively marked will help you decide if it is worth guessing an answer you are unsure about. If you don’t lose marks for being wrong, playing the odds in a multiple-choice test can help you get a better score.
In almost all cases, your score in the numerical reasoning test will be compared against other test takers, including other applicants who have gone for the same role that you are testing for. This means that to be taken further in the process, you will not only have to pass the test, but you will have to perform better than other people.
You might be able to find out the score that you need to get before you take the test, but the best course of action is to perform as well as you can. Get practice tests and make time for revision so that you have the best chance to get a good score on your numerical reasoning test.
Major companies use a variety of providers for their numerical reasoning tests. The provider used generally depends on the overall format of the company’s recruitment process and the other abilities they are assessing as part of their overall selection process.
Employers use the results from a numerical reasoning test to determine whether you can work with numerical information to solve problems.
Candidates that score highly in a numerical reasoning test are likely to be able to deal with numerical information in their day-to-day job and use this effectively to solve numerically related problems.
To improve your numerical reasoning, it is important to become comfortable using numerical information.
Refresh your knowledge of basic mathematical concepts such as calculating percentages or working with fractions or ratios. Use this knowledge when practicing numerical tests.
It is important to remember that a numerical reasoning test assesses your working knowledge of putting into practice basic mathematical concepts. To improve your numerical reasoning, you need to practice using the concepts.
A numerical reasoning test measures a candidate’s ability to work with numerical data to solve problems. You need to have a good grasp and understanding of basic mathematical principles and concepts such as how to calculate percentages or work out ratios.
If you can understand the information given in the question and which mathematical concept to use to solve the problem, using a calculator app can help to solve the questions in a numerical reasoning test.
If you are unsure of an answer, mark your best guess and then move on. The more questions you answer correctly, the higher your overall score will be.
Numerical reasoning tests are designed to assess how well candidates can interpret numerical data to solve problems. These tests are timed tests. The timed nature of the test adds an extra element of pressure to the assessment which some candidates find challenging.
Many questions also require candidates to use multiple calculations or principles to solve the problem, adding additional challenges when completing the test.
Many employers provide details of practice numerical reasoning tests on their websites.
In addition, JobTestPrep has a range of practice numerical reasoning tests. These tests enable you to gain an understanding of what a numerical test is, practice realistic questions and become familiar with the format and the style of questioning used in many numerical reasoning tests used by employers.
Practicing numerical reasoning tests is essential to enable you to become familiar with how questions are laid out and help you identify any gaps in your mathematical knowledge that you need to work on before sitting the actual test.
When practicing it is important to practice under timed conditions so you simulate the time pressure that you will feel when sitting the test.
Numerical reasoning tests are ability tests that focus on evaluating a candidate’s numerical ability. Specifically, the test measures a candidate’s aptitude to use and interpret numerical information to solve problems. Questions are presented in the form of graphs, tables or charts, candidates use their understanding of mathematical concepts to solve the problem presented. An IQ test is a general test that evaluates a candidate’s overall intelligence through the use of various tests.
Numerical reasoning tests are designed to determine a candidate’s aptitude in dealing with numbers to interpret numerical information and solve problems. The tests require you to use your understanding of basic mathematical principles to solve numerically related problems.
The tests assess your numerical ability, how to approach using use numerical information and whether can use your mathematical knowledge to logically solve a problem rather than whether are good at math.
WikiJob has several resources and tips to help you prepare for your numerical reasoning test. These include information on what a numerical test is, the types of questions you can encounter when completing a numerical reasoning test and top tips on how to pass numerical aptitude questions.
Also look at JobTestPrep for great resources for practicing test questions.
Each employer will stipulate their conditions for candidates who fail the numerical reasoning test.
To ensure that you perform to the best of your ability when sitting a numerical reasoning test, it is important to practice the tests and refresh your memory on any gaps in your knowledge of basic mathematic principles.
When sitting the actual test, remain calm and ensure you read the question carefully. Don’t dwell too long on a question, make an educated guess then move on to the next question.
Each employer will have its own format and structure for a numerical reasoning test. Some SHL tests enable screen recording, this is dependent on the employer and format of the test being administered.
Before taking the test it is advisable to contact the recruiter with any questions you have and how the results will be captured.
Integrity is an important quality for all employers. When taking a numerical reasoning test, it is vital to be honest and approach the test in a positive frame of mind.
Numerical reasoning tests assess a candidate’s ability to work with numerical information. This ability is generally assessed multiple times throughout the recruitment process.
Ensuring you have practiced the tests and can perform to the best of your ability in the test is essential to demonstrate consistent results in an employer’s recruitment process. Any discrepancies in the results are likely to be highlighted and investigated accordingly.
Final Thoughts
Numerical ability tests typically don’t require mathematical skills beyond addition, subtraction, multiplication, division, ratios and percentages. Companies are primarily interested in your grasp of the basics. They’re asking: ‘Is this person confident working with numbers in general?’.
However, you will be expected to perform this sort of arithmetic quickly and accurately. You will be under pressure, both from a strict time limit and from the importance of the test. Though these skills are simple, they need to be second-nature. Practise them until they are.








